Descriptif
Analysis (MAA 102) is an introductory-level mathematical analysis course which provides a well-balanced approach between foundational notions and calculus. It is designed to equip students with the fundamental analytical tools required to pursue studies in Mathematics and, more generally, in any scientific field (Physics, Mechanics, Economics, Engineering, Computer Science, etc).
Objectifs pédagogiques
The objective is to present fundamental notions and results regarding the set of real and complex numbers, real and complex-valued sequences, real and complex-valued infinite series and functions of one real variable.
With respect to the expected initial knowledge of the students, the Course follows a more systematic approach, providing a few insights on the roots of analysis and proving all important results. Though in the continuity of the students' previous studies in Mathematics, this course may also be a turning point towards more rigor and proofs.
effectifs minimal / maximal:
1/200Diplôme(s) concerné(s)
Format des notes
Numérique sur 20Littérale/grade américainPour les étudiants du diplôme Bachelor of Science de l'Ecole polytechnique
Le rattrapage est autorisé (Note de rattrapage conservée écrêtée à une note seuil de 9)- Crédits ECTS acquis : 5 ECTS
La note obtenue rentre dans le calcul de votre GPA.
Pour les étudiants du diplôme Echanges PEI
Le rattrapage est autorisé (Note de rattrapage conservée écrêtée à une note seuil de 9)- Crédits ECTS acquis : 5 ECTS
La note obtenue rentre dans le calcul de votre GPA.
Programme détaillé
Week I - The Set of Real Numbers
- The construction of the set of Natural numbers
- The construction of the set of Rational numbers
- The construction of the set of Real numbers
- Upper bound and least upper bound properties
Week II - The Set of Complex Numbers
- Intervals
- The integer part of a real number
- The
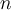-th root of a real number - The set of complex numbers
- Modulus and argument of a complex number
- The 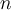-th root of a complex number
Week III - Sequences
- Limite of sequence
- Comparison tests for sequences
- Monotone sequences
Week IV - Sequences
- Infinite limits
- Adjacent sequence
- Subsequences and accumulation points
- The Bolzano-Weierstrass Theorem
Week V - Infinite Series
- Finite and Infinite series
- Convergence Tests
Week VI - Infinite Series
- Convergence tests
- Further tests for convergence
- Absolute convergence of series
- Alternative series
Week VII - MIDTERM
Week VIII - Continuity of a Function of One Variable
- Subsets of
- Limits of functions
- Continuity of a function at a point
Week IX - Continuity of a Function of One Variable
- Continuous functions
- Intermediate Value Theorem
- Uniformly continuous function
Week X - Global Properties of Functions
- Global properties of continuous functions
- Monotone functions
- Periodic functions
Week XI - Differentiability of a Function of One Variable
- Differentiable functions
- The Inverse Function Theorem
- Higher order derivatives
Week XII - Variations of Functions
- Extrema of functions
- Rolle's Theorem and the Mean Value Theorem
- Convex functions
Week XIII - Classical Functions
- Trigonometric functions
- Exponential and logarithm
- Hyperbolic functions
Week XIV - Taylor Expansions
- Taylor-Lagrange's Theorem
- Taylor expansions of classical functions and Taylor series
- Manipulating Taylor expansions
- Applications of Taylor expansions