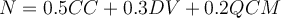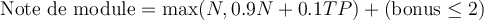Descriptif
Ce cours est une introduction à l'optimisation et au contrôle de modèles dynamiques qui sont des outils indispensables à la conception et au bon fonctionnement des systèmes issus des sciences, de la technologie ou de l'industrie et des services.
La première partie du cours portera sur l'optimisation, avec ou sans contraintes, en dimension finie ou infinie. Après quelques aspects théoriques sur les conditions d'optimalité et l'existence d'optima, l'accent sera mis sur les algorithmes numériques de type gradient. Une attention particulière sera portée à certaines grandes classes de problèmes comme la programmation linéaire et la programmation quadratique séquentielle.
La seconde partie du cours étudiera le contrôle d'équations différentielles modélisant des problèmes d'évolution en temps. Les notions de contrôlabilité, d'état adjoint et le principe du minimum de Pontryaguine seront introduits.
Par delà de ces aspects techniques, le cours se veut aussi une illustration de la démarche des mathématiques appliquées, mélant modélisation, analyse mathématique et simulation numérique, qu'il est nécessaire de maîtriser dans tout processus innovant.
Objectifs pédagogiques
Donner aux étudiants les bases théoriques et pratiques de l'optimisation et du contrôle.
effectifs minimal / maximal:
1/265Diplôme(s) concerné(s)
Objectifs de développement durable
ODD 9 Industrie, Innovation et Infrastructure.Pour les étudiants du diplôme Programmes d'échange internationaux
Pour les élèves ayant effectué leurs études en France : aucun autre prérequis que le niveau de connaissances acquis en classes préparatoires ou en premier cycle universitaire. Pour les autres élèves : algèbre linéaire, calcul différentiel, équations différentielles ordinaires, espaces de Hilbert.
Pour les étudiants du diplôme Titre d’Ingénieur diplômé de l’École polytechnique
Pour les élèves ayant effectué leurs études en France : aucun autre prérequis que le niveau de connaissances acquis en classes préparatoires ou en premier cycle universitaire. Pour les autres élèves : algèbre linéaire, calcul différentiel, équations différentielles ordinaires, espaces de Hilbert.
Format des notes
Numérique sur 20Littérale/grade réduitPour les étudiants du diplôme Programmes d'échange internationaux
Vos modalités d'acquisition :
Le cours est évalué par un examen écrit final de 2 ou 3 heures, un devoir obligatoire (à faire et à rendre de manière individuelle), un contrôle continu par QCM chaque semaine, un TP à rendre (facultatif) et un bonus de 2 points maximum donné par l'enseignant de petites classes. Pour l'examen écrit de la session normale (mai-juin) les documents écrits autorisés sont les suivants à l'exception de tout autre: polycopié du cours, feuilles de PC, notes personnelles. Pour la session de ratrappage ou de septembre, aucun document ne sera autorisé.
avec
- CC = note du contrôle classant
- DV = note du devoir maison obligatoire
- QCM = note moyenne des 9 meilleurs QCM sur 10 (un par séance)
- TP = note du TP à rendre (facultatif)
- Bonus attribué par les enseignants de petites classes en fonction de l'assiduité et de la participation
- Transformation de la note chiffrée en lettre par mes soins (suivant les instructions de la Direction des Etudes sur les quotas de A et B)...
- Crédits ECTS acquis : 5 ECTS
Le coefficient de l'UE est : 10
La note obtenue rentre dans le calcul de votre GPA.
La note obtenue est classante.
Pour les étudiants du diplôme Titre d’Ingénieur diplômé de l’École polytechnique
Vos modalités d'acquisition :
Le cours est évalué par un examen écrit final de 2 ou 3 heures, un devoir obligatoire (à faire et à rendre de manière individuelle), un contrôle continu par QCM chaque semaine, un TP à rendre (facultatif) et un bonus de 2 points maximum donné par l'enseignant de petites classes. Pour l'examen écrit de la session normale (mai-juin) les documents écrits autorisés sont les suivants à l'exception de tout autre: polycopié du cours, feuilles de PC, notes personnelles. Pour la session de ratrappage ou de septembre, aucun document ne sera autorisé.
avec
- CC = note du contrôle classant
- DV = note du devoir maison obligatoire
- QCM = note moyenne des 9 meilleurs QCM sur 10 (un par séance)
- TP = note du TP à rendre (facultatif)
- Bonus attribué par les enseignants de petites classes en fonction de l'assiduité et de la participation
- Transformation de la note chiffrée en lettre par mes soins (suivant les instructions de la Direction des Etudes sur les quotas de A et B)...
- Crédits ECTS acquis : 5 ECTS
Le coefficient de l'UE est : 10
La note obtenue rentre dans le calcul de votre GPA.
La note obtenue est classante.
Programme détaillé
Programme des amphis
amphi 1:
Introduction à l'optimisation, exemples, existence d'optima en dimension finie, analyse convexe.
amphi 2:
Existence d'optima en dimension infinie, calcul différentiel, inéquation d'Euler.
amphi 3:
Conditions d'optimalité avec contraintes d'égalité et d'inégalité.
amphi 4:
Lagrangien, point selle, théorème de Kuhn et Tucker, dualité, algorithme de gradient sans contrainte.
amphi 5:
Algorithmes de gradient avec contraintes (projeté, Uzawa, SQP).
amphi 6:
Programmation linéaire.
amphi 7:
Introduction au contrôle, contrôlabilité des systèmes linéaires, critère de Kalman.
amphi 8:
Contrôle optimal du système linéaire quadratique, état adjoint, équation de Ricatti.
amphi 9:
Contrôle de systèmes non-linéaires, principe du minimum de Pontryaguine.
amphi 10:
Preuve et applications du principe du minimum de Pontryaguine.