Format des notes

Programme détaillé

Brève description des principales notions et résultats du cours :

I - Rappels ou compléments de topologie dans un cadre plus général celui des espaces vectoriels normés. Nous nous pencherons sur les topologies associées à des familles de semi-normes, topologies que nous retrouverons dans l'étude du dual topologique d'un espace de Banach. 

II - Quelques propriétés géométriques et topologiques des sous-ensembles convexes avec des applications telles que, par exemple, les conséquences du Théorème de Helly dont l'énoncé est le suivant "Pour toute famille finie de convexes d'un espace euclidien de dimension 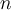, si l'intersection de 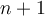quelconques des éléments de cette famille est non-vide, alors l'intersection de tous les éléments de la famille est non-vide".

III - Théorème de Hahn-Banach sous sa forme géométrique (Théorème de séparation des convexes) et sous sa forme analytique (prolongement de formes linéaires). À titre d'illustration, nous montrerons l'existence de la limite de Banach qui est définie sur l'espace des suites bornées, invariante par décalage et qui prolonge l'application "limite" qui est définie sur l'espace des suites qui convergent (au sens usuel). 

Nous termineront cette partie du cours par le Théorème de Krein-Milman qui, en dimension finie, s'énonce sous la forme : "Tout convexe compact d'un espace vectoriel normé de dimension finie est l'enveloppe convexe de l'ensemble de ses points extrémaux". 

III - Les "Grands Théorèmes de l'Analyse Fonctionnelle" : le Théorème de Baire, le Théorème de Banach-Steinhaus, le Théorème de l'application ouverte et enfin, le Théorème du graphe fermé. Tous ces résultats sont les outils de base dans l'étude des espaces vectoriels normés de dimension infinie. 

IV - Étude du dual topologique et du bi-dual topologique d'un espace de Banach. Ceci nous amènera à comprendre les topologies faibles et topologies faibles  qui sont associées à des familles de semi-normes. Nous en profiterons pour introduire également la notion d'espace réflexif. Les topologies faibles  jouent un rôle crucial dans le Théorème de Banach-Alaoglu qui s'énonce sous la forme : "La boule unité fermée (pour la topologie forte) de l'espace dual d'un espace de Banach, est compacte pour la topologie faible ". Nous verrons comment ce résultat donne un cadre naturel à des problèmes de minimisation de fonctionnelles semi-continues-inférieurement, et il nous permettra également de donner une version du Théorème de Krein-Milman en dimension infinie. 

V - Étude des Algèbres de Banach qui permettent de regrouper toute une série de résultats dans un cadre unifié et simple. Nous donnons une démonstration due à Israel Gelfand d'un Théorème très difficile de Norbert Wiener qui stipule que : "Pour toute fonction 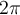périodique 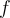dont la série des coefficients de Fourier converge absolument, la série de Fourier de la fonction 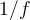converge absolument si et seulement si 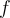ne s'annule pas".

VI - Étude du spectre de certaines classes d'opérateurs définis entre deux espaces de Banach. Définition des opérateurs compacts et pruve de quelques résultats classiques concernant leurs spectres. Ceci nous amènera à l'alternative de Fredholm qui, en dimension infinie, remplace le fait qu'en dimension finie, un endomorphisme est surjectif si et seulement s'il est injectif. Une application classique de ces résultats est l'analyse du spectre des opérateurs elliptiques tels que l'opérateur de Sturm-Liouville en dimension .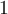

VII. Nous terminerons ce cours par l'étude des Opérateurs de Fredholm ce qui nous permettra d'introduire la notion d'indice de Fredhlom. La notion d'opérateur de Fredholm et celle d'indice de Fredholm sont essentielles dans l'étude des Opérateurs de Toeplitz qui constituent un prototype (simple) de résultats profonds tels que le Théorème d'Atiyah-Singer qui relient des indices d'opérateurs elliptiques à des invariants topologiques des variétés.

Bibliographie : 

- Haïm Brezis, Functional Analysis, Sobolev Spaces and Partial Differential Equations, Universitext, Springer (2010).

- John B. Conway, A Course in Functional Analysis, Graduate Texts in Mathematics, Springer (1990).

- Walter Rudin, Functional Analysis, MacGrow-Hill (1991).

- Barry Simon, Convexity: An Analytic Viewpoint, Cambridge University Press (2011).

- Kôsaku Yosida, Functional Analysis, Springer (1980).